RESEARCH
September 2020
Samuel Laferrière1,2, Marco Bonizzato3, Numa Dancause3, & Guillaume Lajoie1,4 *
1Mila – Québec Artificial Intelligence Institute
2Computer Science Dept., Université de Montréal
3Neuroscience Dept., Université de Montréal
4Mathematics and Statistics Dept., Université de Montréal
*Email: g.lajoie@umontreal.ca
The stimulation optimization problem & the rapid evolution of electrode technology:
The development of neurostimulation techniques for targeted biomarker control is an active area of research. New implantable devices are microfabricated with hundreds or thousands of electrodes, holding great potential for precise spatiotemporal stimulation. These interfaces not only serve as a crucial experimental tool to probe computation in neural circuits [7,8,9], but also have applications in neuroprostheses used to aid recovery of motor, sensory and cognitive modalities affected by injury or disease [14-19]. Yet, existing electrical neuromodulation interventions do not fully take advantage of the rich stimulation repertoire advanced electrode technologies offer, instead relying mostly on incomplete and manual input-output mapping, and often on single electrode stimulation [1,6].
There are two important challenges when designing algorithms to unveil and control neurostimulation-to-evoked-response correspondences. First, effectively searching the space of possible spatiotemporal stimulation patterns (which can include duration, intensity, location, temporal ordering, etc.) is a complex task because of its combinatorial explosion in size. Exhaustive search is therefore impossible in practice, especially if algorithms are to be used on-line in clinical settings. Second, online learning needs to be flexible enough to deal with noise and occasional spurious responses, as well as possible habituation or gradual changes due to plasticity mechanisms in the nervous system. In short what is needed from automated stimulation protocols is both speed (data efficiency) and flexibility (robustness to changes).
One way to be data efficient is to have high-resolution models of the underlying optimization landscape. For targeted biomarker control, the underlying cost function to be optimized can be any function of interest from neural stimulation to a scalar-valued observation, such as physical movement amplitude, max EMG voltage, or in fact any combination of any biomarkers [10-13]. In certain areas, such as spinal cord stimulation, hand-designed model-based optimization has proven effective in some restricted contexts [3, 4], but its scaling potential is limited. For most other applications, such as motor cortex stimulation, our current understanding of input/output properties is too precarious to build effective models. There is thus a need to rely on so-called “black-box” methods, which do not have closed form cost functions to be optimized, but rather only have access to it via point-wise evaluations. Unfortunately, most of these methods, such as random search and genetic algorithms, require too much data to satisfy our first requirement above [5].
Figure 1: Gaussian Process fit for a single EMG activation from single electrode stimulation from an implanted array (discrete x-y coordinates indicate electrode placement). Increasing number of query points shown in green. Surface shows GP’s mean, and color shows standard deviation. Adapted from [1].
Bayesian Optimization & Gaussian Processes:
There is, however, an in between solution: Bayesian optimization (BO), a model-based method. We argue that BO is currently the most promising tool to automate searches for optimal neurostimulation strategies. It permits leveraging prior information, such as expert knowledge, past subjects, known hardware constraints, etc., and combining it with new collected data to update an internal explicit model of stimulation-to-response mappings. Very importantly, BO can be combined with nonparametric models. This means that BO algorithms can learn a model purely from data gathered over the optimization process, making them the ideal fit for finding optimal multi-electrode stimulations both fast, and flexibly.
BO works by constructing a probabilistic surrogate of the cost function at each step, only using its prior and the data that it has acquired so far. An oft-used nonparametric model is Gaussian Processes (GP), which in many cases have closed form posteriors and hence are amenable to online hyperparameter optimization. At each step, given the prior and initial data, the GP model fit is updated and gives a global probabilistic estimate for the true underlying cost function. This estimate contains a measure of uncertainty, which allows tracking, and adapting online to, signal delivery changes caused by implant movements, structural changes in the underlying brain substrate, or even muscle response changes due to fatigue. Crucially however, this uncertainty measure can also be leveraged to decide on the next query point, therefore optimally guiding exploration. This is done through the means of an acquisition function, which evaluates the utility of the possible next queries by turning the probabilistic estimate into a scalar output. This function can then be maximized by deterministic methods. Figure 1 shows the gradual querying and GP fit of an electromyography (EMG) response to single channel stimulation within an implanted electrode array in M1 cortical area of a non-human primate (see [1] for more details).
Scalable neurostimulation optimization: challenges, solutions, and future directions.
BO has already proven its worth in a wide range of applications such as recommender systems, robotics and reinforcement learning, environmental monitoring and sensor networks, automatic hyperparameter tuning, and many more [2]. Nonetheless, BO is not yet a seamless plug-and-play technology, and needs to incorporate neuroscience knowledge in the form of priors in order to adapt it to the spatiotemporal neurostimulation setting. With increasing objective complexity such as the precise coordination of multiple muscle activations, richer spatiotemporal patterns of stimulation are needed. However, the increasing dimensionality of stimulation parameter space (timing, location, amplitude, duration) makes it difficult to resolve with limited queries, even with standard BO approaches. Fortunately, this parameter landscape is very structured due to anatomical and functional organization of the nervous system, and it is possible to make use of this structure to enable scalable approaches.
In a recent article, we propose a GP-based BO approach that leverages acquired knowledge of responses evoked by stimulation of single channels to hierarchically build response models of more complex stimulation patterns [1]. The idea is to first fit stim-to-response GPs for individual channels (see Fig. 1), and then use these as priors for GP models of multi-channel stimulation patterns, where only nonlinear correction terms need to be learned with additional queries. We refer to this process as hierarchical GP-BO since it relies on GP models fitted in lower dimensional spaces to initialize and constrain ones in higher dimensional spaces, where standard sampling would be prohibitively costly. We demonstrated the efficacy of this approach for spatiotemporal stimulation optimization of evoked complex EMG responses, with experiments in the motor cortex (M1) of a non-human primate model implanted with a multielectrode array as depicted in Figure 2 A. This novel approach largely outperforms standard GP-BO as well as random search and crucially, enables a path to scalability to more complex patterns. Figure 2 B,C shows the optimization process for a two-pulse stimulation signal with the objective of co-activating two muscles in a precise sequence.
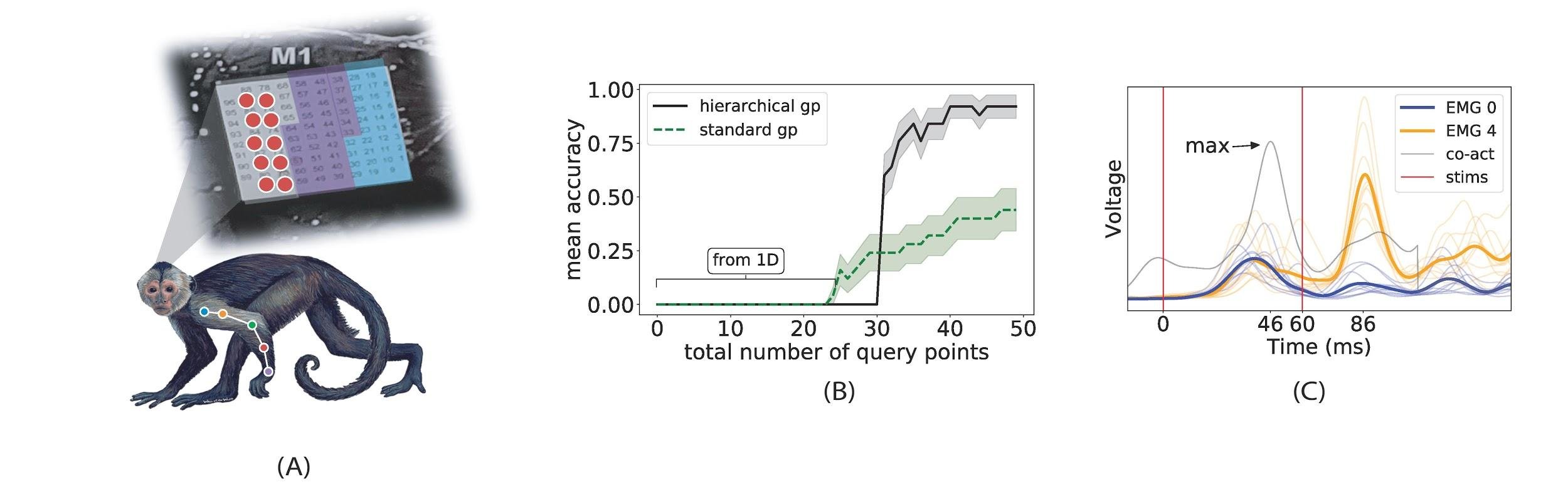
Figure 2: (A) Cebus apella with Utah Array (M1) and implanted muscle EMGs (not real locations). Stimulation search space restricted to 2 × 5 grid in red. (B) Mean Prediction accuracy vs. total number of queries comparing our approach to a standard GP for co-activation of EMGs 0 & 4 with target delay of 40ms. Mean and standard deviation (shaded area) sampled over 10 independent fits. Best performance for standard GP uses 25 random initialization points (shown). Hierarchical GPs uses only 5 random initialization points followed by 25 BO updates in low dimensional spaces (1D). (C) Temporal co-activation found by our method. Thin colored lines show individual muscle responses on 10 distinct trials. Thick lines show mean response. Grey line shows summed translated means, as in A. Red lines show the two stimulation times. Adapted from [1].
References
[1] Laferriere S, Bonizzato M, Cote SL, Dancause N, Lajoie G. Hierarchical Bayesian Optimization of Spatiotemporal Neurostimulations for Targeted Motor Outputs. IEEE Trans Neural Syst Rehabil Eng. 2020;28(6):1452-1460. doi:10.1109/TNSRE.2020.2987001. [2] B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, “Taking the Human Out of the Loop: A Review of Bayesian Optimization,” in Proceedings of the IEEE, vol. 104, no. 1, pp. 148-175, Jan. 2016, doi: 10.1109/JPROC.2015.2494218. [3] Capogrosso M, Milekovic T, Borton D, Wagner F, Moraud EM, Mignardot JB, Buse N, Gandar J, Barraud Q, Xing D, Rey E, Duis S, Jianzhong Y, Ko WK, Li Q, Detemple P, Denison T, Micera S, Bezard E, Bloch J, Courtine G. A brain-spine interface alleviating gait deficits after spinal cord injury in primates. Nature. 2016 Nov 10;539(7628):284-288. doi: 10.1038/nature20118. PMID: 27830790; PMCID: PMC5108412. [4] Zelechowski, M., Valle, G. & Raspopovic, S. A computational model to design neural interfaces for lower-limb sensory neuroprostheses. J NeuroEngineering Rehabil 17, 24 (2020). https://doi.org/10.1186/s12984-020-00657-7 [5] Audet, C., Kokkolaras, M. Blackbox and derivative-free optimization: theory, algorithms and applications. Optim Eng 17, 1–2 (2016). https://doi.org/10.1007/s11081-016-9307-4. [6] Tafazoli, Sina & MacDowell, Camden & Che, Zongda & Letai, Katherine & Steinhardt, Cynthia & Buschman, Timothy. (2020). Learning to Control the Brain through Adaptive Closed-Loop Patterned Stimulation. 10.1101/2020.03.14.992198. [7] Neuromodulation of evoked muscle potentials induced by epidural spinal-cord stimulation in paralyzed individuals. Dimitry G. Sayenko, Claudia Angeli, Susan J. Harkema, V. Reggie Edgerton, and Yury P. Gerasimenko. Journal of Neurophysiology 2014 111:5, 1088-1099. [8] R. Saigal, C. Renzi and V. K. Mushahwar, “Intraspinal microstimulation generates functional movements after spinal-cord injury,” in IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 12, no. 4, pp. 430-440, Dec. 2004, doi: 10.1109/TNSRE.2004.837754. [9] S. L. Côté, A. Hamadjida, S. Quessy, and N. Dancause. Contrasting modulatory effects from the dorsal and ventral premotor cortex on primary motor cortex outputs. The Journal of Neuroscience, 37(24):5960, 06 2017. [10] D. T. Brocker, B. D. Swan, R. Q. So, D. A. Turner, R. E. Gross, and W. M. Grill. Optimized tempo- ral pattern of brain stimulation designed by computational evolution. Science Translational Medicine, 9(371):eaah3532, 01 2017. [11] Moraud EM, Capogrosso M, Formento E, et al. Mechanisms Underlying the Neuromodulation of Spinal Circuits for Correcting Gait and Balance Deficits after Spinal Cord Injury. Neuron. 2016;89(4):814-828. doi:10.1016/j.neuron.2016.01.009. [12] Dalrymple AN, Roszko DA, Sutton RS, Mushahwar VK. Pavlovian control of intraspinal microstimulation to produce over-ground walking. J Neural Eng. 2020;17(3):036002. Published 2020 Jun 2. doi:10.1088/1741-2552/ab8e8e. [13] E. Rouhani and A. Erfanian, “Control of intraspinal microstimulation using an adaptive terminal-based neuro-sliding mode control,” 2015 7th International IEEE/EMBS Conference on Neural Engineering (NER), Montpellier, 2015, pp. 494-497, doi: 10.1109/NER.2015.7146667. [14] Wagner, F.B., Mignardot, J., Le Goff-Mignardot, C.G. et al. Targeted neurotechnology restores walking in humans with spinal cord injury. Nature 563, 65–71 (2018). https://doi.org/10.1038/s41586-018-0649-2 [15] Petrini, F.M., Bumbasirevic, M., Valle, G. et al. Sensory feedback restoration in leg amputees improves walking speed, metabolic cost and phantom pain. Nat Med 25, 1356–1363 (2019). https://doi.org/10.1038/s41591-019-0567-3 [16] Kasten MR, Sunshine MD, Secrist ES, Horner PJ, Moritz CT. Therapeutic intraspinal microstimulation improves forelimb function after cervical contusion injury. J Neural Eng. 2013;10(4):044001. doi:10.1088/1741-2560/10/4/044001 [17] Provenza NR, Matteson ER, Allawala AB, et al. The Case for Adaptive Neuromodulation to Treat Severe Intractable Mental Disorders. Front Neurosci. 2019;13:152. Published 2019 Feb 26. doi:10.3389/fnins.2019.00152 [18] Chandrasekaran S, Nanivadekar AC, McKernan G, et al. Sensory restoration by epidural stimulation of the lateral spinal cord in upper-limb amputees. Elife. 2020;9:e54349. Published 2020 Jul 21. doi:10.7554/eLife.54349 [19] Flesher SN, Collinger JL, Foldes ST, et al. Intracortical microstimulation of human somatosensory cortex. Sci Transl Med. 2016;8(361):361ra141. doi:10.1126/scitranslmed.aaf8083
Author Biographies:
Samuel Laferriere obtained his bachelors in mathematics and computer science from McGill University (2015). He then joined the Montreal Institute for Learning Algorithms and Guillaume Lajoie’s lab at the Université de Montréal, where he developed Bayesian Optimization algorithms for Neurostimulation, and obtained his Master’s degree (2019). In September, he will be starting his PhD in Statistics at the University of British Columbia.
Marco Bonizzato joined Université de Montréal in 2017, where he is an IVADO and TransMedTech Postdoctoral Fellow. He received his B.S. (2009) and M.S. (2011) from University of Pisa and Scuola Superiore Sant’Anna di Pisa, Italy. He obtained his Ph.D. (2017) in Electrical Engineering at the École Polytechnique Fédérale de Lausanne, Switzerland. His doctoral research involved brain-computer interfaces and neurostimulation to restore walking after spinal cord injury. His research interest now includes mechanisms of cortical control and recovery of movement after paralysis and autonomous optimization of neuroprosthetic devices.
Numa Dancause received his Ph.D. (2005) in Molecular and Integrative Physiology at the University of Kansas Medical Center (KUMC). He pursued post-doctorates at KUMC, Kansas, and at the Department of Neurology, University of Rochester Medical Center, NY. He is now full professor at the Department of Neurosciences, Université de Montréal, and member of the Groupe de recherche sur le système nerveux central (GRSNC). His laboratory is interested in how the primary and premotor cortices interact with each other to control movement. They study their reorganization following lesions, such as stroke, and develop methods to manipulate plasticity in order to maximize recovery.
Guillaume Lajoie obtained his PhD in applied mathematics from the University of Washington (UW), Seattle, USA, in 2013. He pursued postdoctoral work as a Bernstein Fellow at the Max Planck Institute for Dynamics and Self-organization, in Goettingen, Germany, and as a WRF Fellow at the UW Institute for Neuroengineering, in Seattle. He is now an associate professor at the University of Montréal, and a core member of Mila – Québec Artificial Intelligence Institute. His research group works at the intersection of AI and Neuroscience, developing tools to better understand biological and artificial neural networks as well as neural interfacing models and algorithms for scientific and clinical use.
