Geometric Deep Learning-Based Classifiers for Motor Imagery Classification using Electroencephalograms

Ce Ju and Cuntai Guan

School of Computer Science and Engineering at Nanyang Technological University

Since changes in sensorimotor rhythms (SMR) occurring within the sensorimotor areas of the brain during motor imagery (MI) can effectively function as control signals for electroencephalography (EEG)-based brain-computer interfaces (BCIs), MI-EEG classification has been a primary area of research in BCIs [1, 2]. During the planning and execution of movements, SMRs exhibit amplitude changes referred to as the event-related desynchronization/synchronization (ERD/ERS) effects [1]. ERD signifies a reduction in rhythmic activity, while ERS signifies an increase. These patterns are detectable, enabling the precise classification of EEG signals. However, several factors make MI-EEG classification a challenging task. These factors include the volume conduction effect, physiological artifacts in signals, electrode impedance, signal nonstationarity within/between sessions or subjects, and more [3].

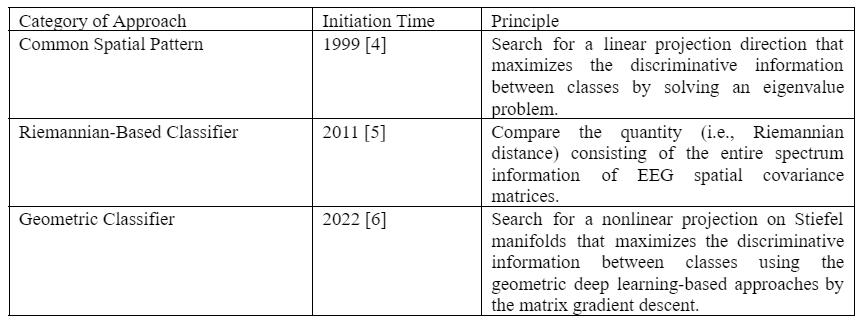
Early MI-EEG classifiers utilized spatial filters, specifically common spatial patterns [4], significantly improving the signal-to-noise ratio when analyzing individual trials. Common spatial patterns rely on second-order statistics of EEG signals, notably the EEG spatial covariance matrix. EEG spatial covariance matrices contain valuable discriminative information, encompassing variance in the on-diagonal entries and the coherence between adjacent channels recorded in the off-diagonal entries. This information is based on tracking the ERD/ERS effect in MI-EEG tasks through frequency analysis techniques, which measure rhythmic oscillations. Subsequently, Barachant introduced using symmetric and positive definite (SPD) manifolds equipped with the affine-invariant Riemannian metric to characterize EEG spatial covariance matrices in a Riemannian-based classification framework called the Riemannian-based classifier [5]. The SPD manifolds-modeling method emphasizes matrix symmetry and positive definiteness of EEG spatial covariance matrices, thereby preserving the spectral power of EEG signals, which is crucial in MI-EEG classification.

The category of classifiers we propose is a natural extension of the common spatial pattern method and the Riemannian-based classifier into the deep learning era. We refer to this category as the geometric MI-EEG classifier, short for the geometric classifier. The most significant difference between our geometric classifiers and other deep learning-based MI-EEG classifiers is that our neural network models utilize EEG spatial covariance matrices, whereas they employ EEG time series. Table 1 presents the MI-EEG classifiers based on EEG spatial covariance matrices. 

Table 1: MI-EEG classifiers based on EEG spatial covariance matrices. 

The basic neural network architecture of the geometric classifier is based on deep neural networks on SPD manifolds, typically within the geometric deep learning category [6,7]. In particular, the BiMap layer within the architecture behaves as a spatial filter and mitigates the impact of volume conduction on the spatial level. Exploiting the discriminative information that can be extracted in the time, space, and frequency (spectral) domains based on the task’s characteristic (the time-space-frequency principle), we propose the following two specific classifiers:

 

• Tensor-CSPNet [8]: It is the first geometric classifier for the general MI-EEG task, employing the time-space-frequency principle. It starts by segmenting the EEG time series in the frequency and time domains based on task characteristics, transforming them into EEG spatial covariance matrices, and concatenating them into the four-dimensional tensor. Then, it utilizes deep neural networks on SPD manifolds to sequentially extract information in the spatial/frequency and time domains. Architecture refers to Figure 1.

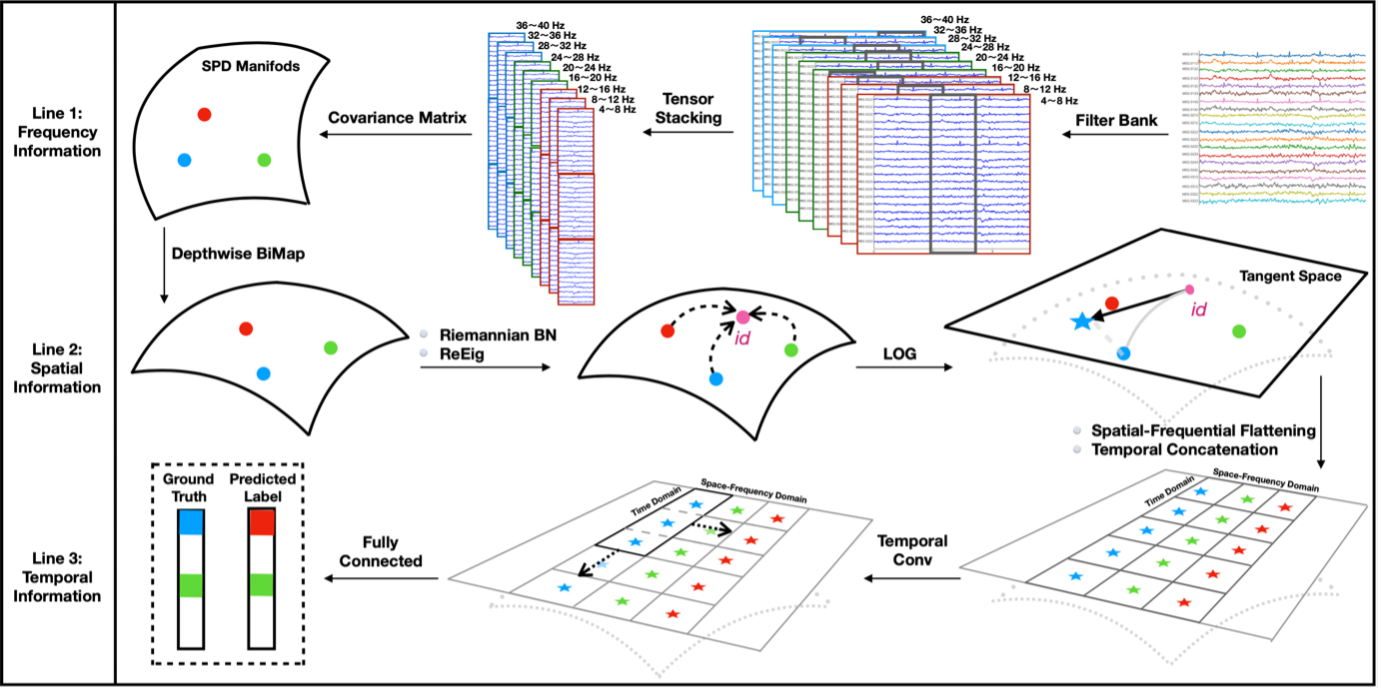
Figure 1: Architecture of Tensor-CSPNet. Figure is extracted from [8].

 

• Graph-CSPNet [9]: It is a geometric classifier rooted in the time-space-frequency principle while considering the signal’s time-frequency theory. It leverages the essence of graph convolutional neural networks to offer a novel geometric deep learning approach for analyzing and processing four-dimensional tensors composed of EEG spatial covariance matrices extracted from the non-uniform segments in the time-frequency domain. The graph-based modeling approach offers a natural way to connect non-uniform EEG segments, facilitating the transmission of spectral information from different time and frequency windows in a specific direction. It extracts information from spatial/frequency and time domains simultaneously. Architecture refers to Figure 2.

  

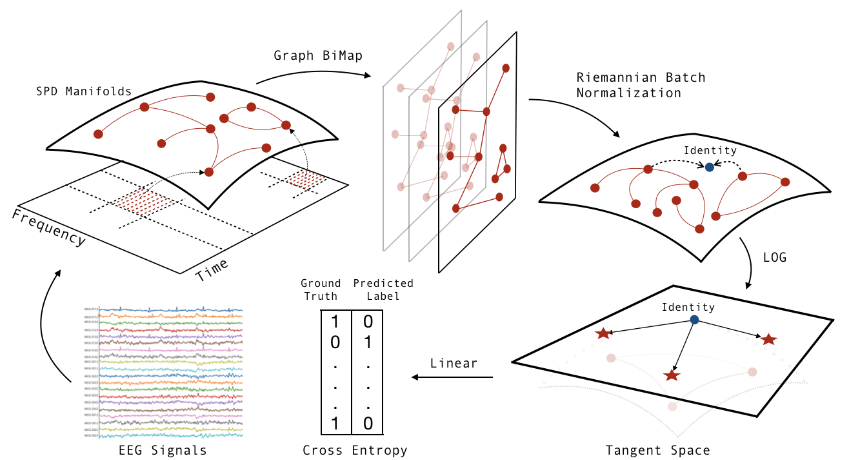
Figure 2: Architecture of Graph-CSPNet. Figure is extracted from [9]. 

 

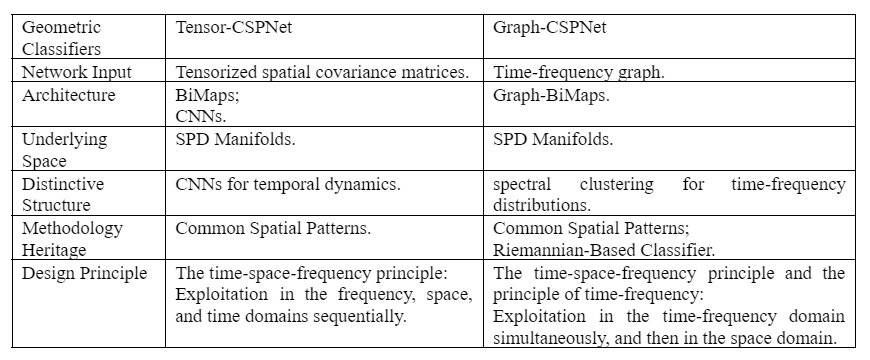
The common key element in both approaches is the BiMap structure within the network architecture, which preserves the discriminative spectral powers between task classes. However, their architectural distinctions are notable in how they capture temporal and frequency (spectral) information. Tensor-CSPNet employs convolutional neural networks (CNNs) to capture temporal dynamics, whereas Graph-CSPNet leverages graph-based modeling to extract discriminative information from the time-frequency domains. A comparison of these two approaches is presented in the table below (Table 2):

                       Table 2: Comparison Between Tensor-CSPNet and Graph-CSPNet.

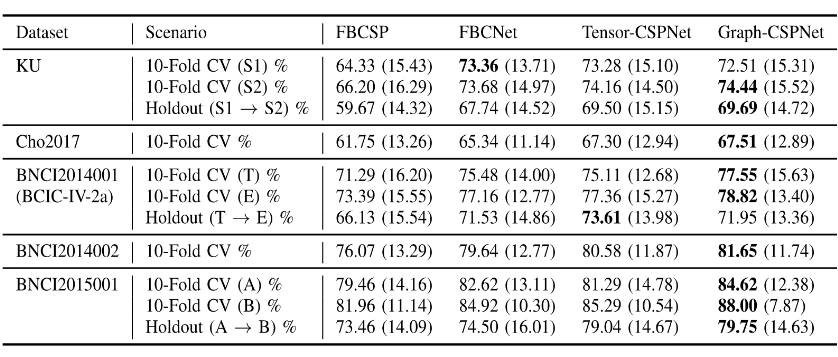
The proposed geometric classifiers have shown strong performance in 11 subject-specific scenarios across the five most commonly used MI-EEG datasets, as seen in Table 3. Among the baseline methods, Filter Bank Common Spatial Patterns (FBCSP) [10], a variant of CSP, is the top-performing CSP classifier using EEG spatial covariance matrices, and FBCNet [11] is one of the leading deep learning-based classifiers using EEG time series. It’s important to note that the proposed geometric classifiers are deep learning-based classifiers using EEG spatial covariance matrices, not EEG time series. Therefore, this new category of MI-EEG classifiers inherits the mechanism of conventional CSP-based classifiers using the BiMap structure and outperforms other neural network-based MI-EEG classifiers in the deep learning era. For more experimental results of geometric classifiers, please refer to [8,9].

Table 3: Average accuracies and their corresponding standard deviations obtained from subject-specific analyses of the KU, CHO2017, BNCI2014001, BNCI2014002, and BNCI2015001 datasets. Each entry in the table represents the mean accuracy and its associated standard deviation. Importantly, the best-performing result for each analysis is emphasized in bold, offering a more prominent visual representation of the optimal metrics. Data are extracted from [8] and [9].

Finally, the corresponding GitHub repository for Tensor-CSPNet and Graph-CSPNet  refers to https://github.com/GeometricBCI/Tensor-CSPNet-and-Graph-CSPNet.

In sum, these novel categories of geometric deep learning-based MI-EEG classifiers offer an alternative solution in the era of deep learning different from those commonly used CNN-based solutions [11-13], such new geometric classifiers providing a fresh geometric perspective that injects new vigor into research within this domain by incorporating technical tools from theoretical mathematics and physics and has paved the way for a novel approach to tackling MI-EEG tasks [14-19].

 

Acknowledgements:

This work was supported in part by the RIE2020 Industry Alignment Fund–Industry Collaboration Projects (IAF-ICP) and in part by the RIE2020 Advanced Manufacturing and Engineering (AME) Programmatic Grant, Singapore, under Grant A20G8b0102.

The authors express their gratitude to Prof. Yuxiao Yang of Zhejiang University, China, for providing valuable feedback on the manuscript.

 

References:

1. G.Pfurtscheller and FL. Da Silva, “Event-related EEG/MEG synchronization and desynchronization: basic principles,” in Clinical neurophysiology,1999; 110(11):1842-57.
2. G. Pfurtscheller and C. Neuper, “Motor imagery and direct brain-computer communication,” in Proceedings of the IEEE, 2001; 89(7):1123-34.
3. F. Lotte, et al., “A review of classification algorithms for EEG-based brain–computer interfaces,” in Journal of neural engineering, 2007; 31;4(2):R1.
4. J. Müller-Gerking, et al., “Designing optimal spatial filters for single-trial EEG classification in a movement task,” in Clinical neurophysiology,1999; 110(5):787-98.
5. A. Barachant, et al., “Multiclass brain–computer interface classification by Riemannian geometry, ” in IEEE Transactions on Biomedical Engineering, 2011; 59(4):920-8.
6. Z. Huang and L. Van Gool, “A riemannian network for spd matrix learning,” In Proceedings of the AAAI conference on artificial intelligence 2017; (Vol. 31, No. 1).
7. Daniel, Brooks, et al., “Riemannian batch normalization for SPD neural networks,” in Advances in Neural Information Processing Systems 32, 2019.
8. C. Ju and C. Guan. “Tensor-cspnet: A novel geometric deep learning framework for motor imagery classification,” in IEEE Transactions on Neural Networks and Learning Systems. 2022; DOI:10.1109/TNNLS.2022.3172108.
9. C. Ju and C. Guan, “Graph Neural Networks on SPD Manifolds for Motor Imagery Classification: A Perspective From the Time–Frequency Analysis,” in IEEE Transactions on Neural Networks and Learning Systems, 2023; DOI:10.1109/TNNLS.2023.3307470.
10. Ang, Kai Keng, et al. “Filter bank common spatial pattern (FBCSP) in brain-computer interface.” 2008 IEEE international joint conference on neural networks (IEEE world congress on computational intelligence). IEEE, 2008.
11. Mane, Ravikiran, et al. “FBCNet: A multi-view convolutional neural network for brain-computer interface.” arXiv preprint arXiv:2104.01233 (2021).
12. Lawhern, Vernon J., et al. “EEGNet: a compact convolutional neural network for EEG-based brain–computer interfaces,” in Journal of neural engineering, 2018; 15.5 (2018): 056013.
13. Schirrmeister, Robin Tibor, et al. “Deep learning with convolutional neural networks for EEG decoding and visualization,” in Human brain mapping, 2017;  38.11 (2017): 5391-5420.
14. C. Ju, et al., “Federated Transfer Learning for EEG Signal Classification,” in 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society, 2020, pp. 3040-3045, DOI: 10.1109/EMBC44109.2020.9175344.
15. C. Ju, Kobler Reinmar, and C. Guan., “Score-Based Data Generation for EEG Spatial Covariance Matrices: Towards Boosting BCI Performance,” In 2023 45nd annual international conference of the IEEE engineering in medicine & biology society (EMBC), 2023.
16. C. Ju and C. Guan, “Deep Optimal Transport for Domain Adaptation on SPD Manifolds.” arXiv preprint arXiv:2201.05745, 2022.
17. Kobler, Reinmar, et al. “SPD domain-specific batch normalization to crack interpretable unsupervised domain adaptation in EEG,” in Advances in Neural Information Processing Systems, 2022; 35:6219-6235.
18. Pan, Yue-Ting, Jing-Lun Chou, and Chun-Shu Wei, “MAtt: a manifold attention network for EEG decoding,” in Advances in Neural Information Processing Systems, 2022; 35:31116-31129.
19. Bonet, Clément, et al. “Sliced-wasserstein on symmetric positive definite matrices for m/eeg signals.” International Conference on Machine Learning. PMLR, 2023.

 

Author Biography

 

Ce Ju is a PhD candidate at Nanyang Technological University, Singapore. He has worked with the Intelligent Driving Group at Baidu Inc., Beijing, China, and the Artificial Intelligence Department at WeBank Company, Ltd., Shenzhen, China.  He has also been a visiting scholar at the Fields Institute for Research in Mathematical Sciences, Toronto, Canada, and the Advanced Telecommunications Research Institute International, Kyoto, Japan. He holds 47 granted patents and has 12 patents currently under substantive examination in China. His research interests include geometric methods in engineering, optimal transport, machine learning, and neural signal processing.

 

 

Cuntai Guan (Fellow IEEE) received his Ph.D. from Southeast University, China 1993. He is a President’s Chair Professor at the School of Computer Science and Engineering, Nanyang Technological University, Singapore. He is the Director of the Artificial Intelligence Research Institute, Director of the Centre for Brain-Computing Research, and the Co-Director of S-Lab for Advanced Intelligence. His research interests include brain-computer interfaces, machine learning, medical signal and image processing, artificial intelligence, and neural and cognitive rehabilitation. He is a recipient of the Annual BCI Research Award (first prize), King Salman Award for Disability Research, IES Prestigious Engineering Achievement Award, Achiever of the Year (Research) Award, and Finalist of President Technology Award. He is also an elected Fellow of the US National Academy of Inventors (NAI), the Academy of Engineering Singapore (SAEng), and the American Institute for Medical and Biological Engineering (AIMBE).